买卖股票

最近做了一个动规算法题（1911），发现有一个买卖股票系列很值得循序渐进地上手动规，于是做了做 汇总了一下。

LeeCode教你学炒股：

1.买卖股票的最佳时机

2.买卖股票的最佳时机 II

3.买卖股票的最佳时机 III

4.买卖股票的最佳时机 IV

5.买卖股票的最佳时机含手续费

6.最佳买卖股票时机含冷冻期

最后做一下1911，会发现简单好多

121. 买卖股票的最佳时机

只有一次购入和一次出售，找到一个最大利润方案。

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {
    let now = -prices[0], // 假设如果第一天买入，手里还有这么多钱（负成本）
    	max = 0 // 假设第一天买了接着卖出，利润为0（利润初始值）
    for (let i = 0, len = prices.length; i < len; i++) {
        now = Math.max(now, -prices[i]) // 目前手里还有多少钱  其实是找一个最低成本
        max = Math.max(max, prices[i] + now) // 最大利润  找一个最大的价钱，减去最小成本
    }
    return max
};

122. 买卖股票的最佳时机 II

可以有多次购入和售出，没有次数限制，找到一个最大利润和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {    
    let max = 0,
        cost = -prices[0] // 负利润
    for (let i = 0, len = prices.length; i < len; i++) {
        // 实在是难设计，实在是妙啊！
        max = Math.max(max, prices[i] + cost) // 关系1：利润 = 当前价格 - 成本
        cost = Math.max(cost, max - prices[i]) // 关系2：成本 = 当前价格 - 利润
    }

    return max
};

123. 买卖股票的最佳时机 III

最多两次购入和售出，直到一个最大利润和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {
    // 分析状态 - 啥都没买、买了一股、卖了一股、没有操作、买了第二股、卖了第二股
    // 根据状态分析变量 - 买一的钱、卖一的钱、买二的钱、卖二的钱
    // 确定边界值↓全都当做第一次就买入卖出
    let buy1 = -prices[0], 
        sell1 = 0, 
        buy2 = -prices[0], 
        sell2 = 0
    // 枚举
    for (let i = 0, len = prices.length; i < len; i++) {
        // 根据每个变量的公式进行枚举
        buy1 = Math.max(buy1, -prices[i]) // 最少的买入钱
        sell1 = Math.max(sell1, buy1 + prices[i]) // 最多的卖出钱 - 最少的买入钱
        buy2 = Math.max(buy2, sell1 - prices[i]) // 最多的买二之后剩下的钱
        sell2 = Math.max(sell2, buy2 + prices[i]) // 最多的卖出钱 + 剩下的钱
    }

    return sell2
};

188. 买卖股票的最佳时机 IV

先扔一端通不过的代码，我好菜啊

image-20230711203442875

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * @param {number} k
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(k, prices) {
    // 有一个不受次数限制的情况
    function hasNoLimit(nums) {
        let cost = -nums[0],
            max = 0
        for (let i = 0, len = nums.length; i < len; i++) {
            cost = Math.max(cost, max - nums[i])
            max = Math.max(max, cost + nums[i])
        }
        return max
    }

    // 去掉一个特殊情况
    if (!prices.length) {
        return 0
    }

    // 去掉另一个情况
    if(k >= prices.length / 2) {
        return hasNoLimit(prices)
    }

    // 开一个长度为k的变量二维数组
    let dp = new Array(k).fill(new Array(2).fill(0))
    dp[0][0] = -prices[0]
    dp[0][1] = 0

    
    for (let i = 1, len = prices.length; i < len; i++) {
        for (let j = 1; j < k; j++) {
            dp[j][0] = Math.max(dp[j - 1][0], dp[j - 1][1] - prices[i])
            dp[j][1] = Math.max(dp[j - 1][1], dp[j][0] + prices[i])
        }
    }

    return dp[k - 1][1]
};

算了一遍测试用例，似乎是次数把控的问题。

受不了了，理应我说理应，无论多少次，都是那么个状态表达式，但是就不行，但是我找不出错来！然后没辙了分情况吧，还有有一些臭臭长长的测试用例通不过！！！！！啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊！！！！！

image-20230711212016410

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
/**
 * @param {number} k
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(k, prices) {
    // 有一个不受次数限制的情况
    function hasNoLimit(nums) {
        let cost = -nums[0],
            max = 0
        for (let i = 0, len = nums.length; i < len; i++) {
            cost = Math.max(cost, max - nums[i])
            max = Math.max(max, cost + nums[i])
        }
        return max
    }
    // 有一个仅限两次的情况
    function hasOnlyTwo(nums) {
        let buy1 = -nums[0], buy2 = -nums[0]
        let sell1 = 0, sell2 = 0
        for (let i = 0, len = nums.length; i < len; i++) {
            buy1 = Math.max(buy1, -nums[i])
            sell1 = Math.max(sell1, buy1 + nums[i])
            buy2 = Math.max(buy2, sell1 - nums[i])
            sell2 = Math.max(sell2, buy2 + nums[i])
        }
        return sell2
    }
    // 有一个仅限一次的情况
    function hasOnlyOne(nums) {
        let cost = -nums[0]
        let max = 0
        for (let i = 0, len = nums.length; i < len; i++) {
            cost = Math.max(cost, -nums[i])
            max = Math.max(max, nums[i] + cost)
        }
        return max
    }

    // 空数组，排除
    if (!prices.length) {
        return 0
    }
    // 无限次，换方法
    if(k >= prices.length / 2) {
        return hasNoLimit(prices)
    }
    // 仅限一次，换方法
    if (k === 1) {
        return hasOnlyOne(prices)
    }
    // 仅限两次，换方法
    if (k === 2) {
        return hasOnlyTwo(prices)
    }

    // 开一个长度为k的变量二维数组
    let dp = new Array(k + 1).fill([-prices[0], 0])
    
    for (let i = 0, len = prices.length; i < len; i++) {
        for (let j = 1; j <= k; j++) {
            dp[j][0] = Math.max(dp[j - 1][0], dp[j - 1][1] - prices[i])
            dp[j][1] = Math.max(dp[j - 1][1], dp[j][0] + prices[i])
        }
    }

    return dp[k - 1][1]
};

明天再看看，太难顶了。

最终看了一眼题解，果然漏了一步↓

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * @param {number} k
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(k, prices) {
    let len = prices.length
    k = Math.min(k, Math.floor(len / 2)) // k >len/2时，实际上是不限次数的，为什么呢？自己想！

    let buy = new Array(len).fill(0).map(() => new Array(k + 1).fill(0)), // 注意这种初始化写法
        sell = new Array(len).fill(0).map(() => new Array(k + 1).fill(0))

    buy[0][0] = -prices[0]
    sell[0][0] = 0
    for (let i = 1; i <= k; i++) { // 给所有次数的buy和sell都初始化一下
        buy[0][i] = -Infinity
        sell[0][i] = -Infinity
    }

    for (let i = 1; i < len; i++) {
        buy[i][0] = Math.max(buy[i - 1][0], sell[i - 1][0] - prices[i])
        for (let j = 1; j <= k; j++) {
            buy[i][j] = Math.max(buy[i - 1][j], sell[i - 1][j] - prices[i])
            sell[i][j] = Math.max(sell[i - 1][j], buy[i - 1][j - 1] + prices[i])
        }
    }

    return Math.max(...sell[len - 1])
};

714. 买卖股票的最佳时机含手续费

无限次，但是每次售出要交手续费。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * @param {number[]} prices
 * @param {number} fee
 * @return {number}
 */
var maxProfit = function(prices, fee) {
    let cost = -prices[0]
    let max = 0
    for (let i = 0, len = prices.length; i < len; i++) {
        cost = Math.max(cost, max - prices[i])
        max = Math.max(max, cost + prices[i] - fee)
    }
    return max
};

309. 最佳买卖股票时机含冷冻期

买卖不限次数，但是卖后的一天不能接着买，美其名曰“冷冻期”。

动态规划

状态：手里攥着股票，手里没攥股票

状态情况分析：

  • 手里攥着股票：今天刚买；昨天买了今天啥事没干
  • 手里没攥股票：今天刚卖，昨天卖了今天搁这冷冻

状态变量分析：

  • 手里剩的钱：昨天计算出来剩的钱/今天就买计算出来剩的钱（买前的钱应该是前天的）
  • 卖出之后挣的钱：昨天计算出来挣的钱/今天就卖计算出来挣的钱（卖前的钱应该是截止到昨天剩的）

状态转移表达式：

剩后 = max(昨日剩后, 前日挣后 - 价钱)

挣后 = max(昨日挣后, 昨日剩后 + 价钱)

临界值：

涉及到跨一天，so

  • 初始天：当天买当天卖 剩后=-价钱 挣后=0
  • 第二天：与初始天的两变量比出较大值 剩后=-价钱(昨天不如不买，今天买)/昨天的剩后 挣后=(今天啥也不干)0/(不如今天卖)价钱+昨日剩
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {
    let len = prices.length
    if(len < 2) {
        return 0
    }

    let dp = new Array(len) 
    dp[0] = [-prices[0], 0]
    dp[1] = [Math.max(dp[0][0], -prices[1]), Math.max(dp[0][1], dp[0][0] + prices[1])]

    for (let i = 2; i < len; i++) {
        dp[i] = [Math.max(dp[i-1][0], dp[i-2][1] - prices[i]), Math.max(dp[i-1][1], dp[i-1][0] + prices[i])]
    }

    return dp[len - 1][1]
};

说真的，一复杂了我就设计不出来，没办法准确找到变量之间的关系

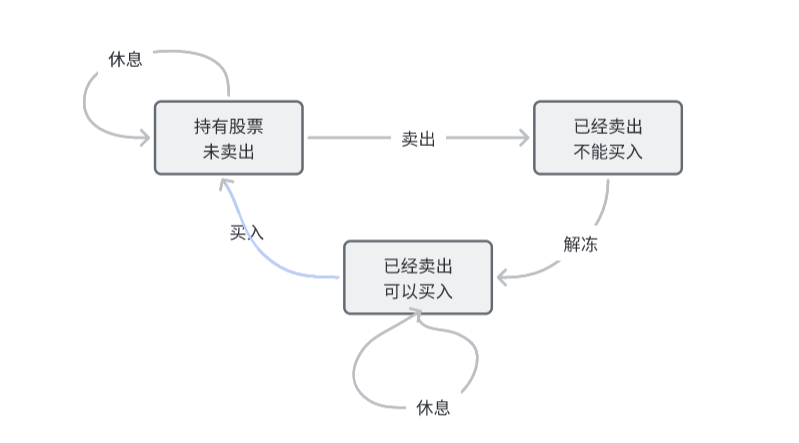
状态机

题解里看到的一个新方法↑↓

状态机四要素：状态、条件、动作、转换

该题状态机图解：

image-20230712152616080

定义三个关键变量：当前手中持有的钱、当前卖出后持有的钱、一次买卖结束后持有的钱。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {
    let hold = -prices[0],
        sold = 0,
        rest = 0
    for (let i = 0, len = prices.length; i < len; i++) {
        let preHold = hold,
            preSold = sold
        hold = Math.max(preHold, rest - prices[i])
        sold = Math.max(preSold, preHold + prices[i])
        rest = Math.max(preSold, rest)
    }
    return Math.max(rest, sold)
};

拓展巩固

1911. 最大子序列交替和

状态：加了，减了

状态关系：加了该减，减了该加

特殊：仅需奇数个数字，因为加后减就变小了

状态方程：和 = 减后的和 + 新数 减后的和 = 和 - 新数

临界值：和 = 第一个数 减后的和 = 0 (第一个数+-)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * @param {number[]} nums
 * @return {number}
 */
var maxAlternatingSum = function(nums) {
    let ans = nums[0]
    let dec = 0

    // 奇数个数就够用，因为根本不可能后面再减一个
    for (let i = 0, len = nums.length; i < len; i++) {
        ans  = Math.max(ans, dec + nums[i]) // 减后面紧接着是加，看看哪个加后更大
        dec = Math.max(dec, ans - nums[i]) // 加后面紧接着是减，看看哪个减后更大
    }

    return ans
};

931. 下降路径最小和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @param {number[][]} matrix
 * @return {number}
 */
var minFallingPathSum = function(matrix) {
    const col = matrix[0].length
    const row = matrix.length

    for (let i = 1; i < row; i++) {
        matrix[i][0] += Math.min(matrix[i-1][0], matrix[i-1][1])
        matrix[i][col-1] += Math.min(matrix[i-1][col-1], matrix[i-1][col-2])
        if (col <= 2) {
            continue
        }

        for (let j = 1; j < col - 1; j++) {
            matrix[i][j] += Math.min(matrix[i-1][j-1], matrix[i-1][j], matrix[i-1][j+1])
        }
    }

    return Math.min(...matrix[row - 1])
};