二分查找

704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function search(nums: number[], target: number): number {
    let left:number = 0
    let right:number = nums.length - 1

    while(left <= right) {
        let mid:number = Math.floor((right-left)/2)+left
        let num:number = nums[mid]
        
        if(target == num) {
            return mid
        } else if (target > num) {
            left = mid + 1
        } else if (target < num) {
            right = mid - 1
        }
    }
    return -1
};

278. 第一个错误的版本

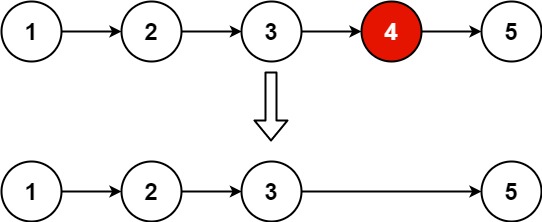
你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例 1：

输入：n = 5, bad = 4
输出：4
解释：
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。
示例 2：

输入：n = 1, bad = 1
输出：1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/** 
 * Forward declaration of isBadVersion API.
 * @param   version   your guess about first bad version
 * @return 	 	      true if current version is bad 
 *			          false if current version is good
 * func isBadVersion(version int) bool;
 */

func firstBadVersion(n int) int {
    left, right := 0, n
    for left < right {
        mid := left + (right-left)/2
        if isBadVersion(mid) {
            right = mid
        } else {
            left = mid + 1
        }
    }
    return right
}

35. 搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func searchInsert(nums []int, target int) int {
    left, right := 0, len(nums)-1
    for left <= right {
        mid := left+(right-left)/2
        num := nums[mid]
        if target == num {
            return mid
        } else if target > num {
            left = mid + 1
        } else if target < num {
            right = mid - 1
        }
    }
    return left
}

双指针

977. 有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]
示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func sortedSquares(nums []int) []int {
    left,right,i := 0,len(nums)-1,len(nums)-1
    arr := make([]int, len(nums))

    for(left <= right) {
        leftVal := nums[left]*nums[left]
        rightVal := nums[right]*nums[right]
        
        if(leftVal > rightVal) {
            arr[i] = leftVal
            left++
        } else {
            arr[i] = rightVal
            right--
        }
        i--
    }
    return arr
}

189. 轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

1
2
3
4
5
6
7
8
9
10
11
12
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {void} Do not return anything, modify nums in-place instead.
 */
var rotate = function(nums, k) {
    while(k > 0) {
        nums.unshift(nums.pop());
        k--;
    }
    return nums;
};

283. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:

输入: nums = [0]
输出: [0]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func moveZeroes(nums []int)  {
    cnt, low, fast := 0, 0, 0
    for fast < len(nums) {
        if nums[fast] == 0 {
            fast++
            cnt++
        } else {
            nums[low] = nums[fast]
            low++
            fast++
        }
    }

    i := len(nums)-cnt
    for i < len(nums) {
        nums[i] = 0
        i++
    }
}

167. 两数之和 II - 输入有序数组

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3：

输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func twoSum(numbers []int, target int) []int {
    left, right := 0, len(numbers)-1
    for left < right {
        lVal, rVal := numbers[left], numbers[right]
        sum := lVal+rVal
        if sum == target {
            return []int{left+1, right+1}
        } else if(sum > target) {
            right--
        } else {
            left++
        }
    }
    return []int{-1, -1}
}

344. 反转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

示例 1：

输入：s = [“h”,”e”,”l”,”l”,”o”]
输出：[“o”,”l”,”l”,”e”,”h”]
示例 2：

输入：s = [“H”,”a”,”n”,”n”,”a”,”h”]
输出：[“h”,”a”,”n”,”n”,”a”,”H”]

1
2
3
4
5
6
7
8
9
10
func reverseString(s []byte)  {
    start, end := 0, len(s)-1
    for start < end {
        temp := s[start]
        s[start] = s[end]
        s[end] = temp
        start++
        end--
    }
}

557. 反转字符串中的单词 III

给定一个字符串 s ，你需要反转字符串中每个单词的字符顺序，同时仍保留空格和单词的初始顺序。

示例 1：

输入：s = “Let’s take LeetCode contest”
输出：”s’teL ekat edoCteeL tsetnoc”
示例 2:

输入： s = “God Ding”
输出：”doG gniD”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func reverseWords(s string) string {
    end,cnt := 0, 0
    arr := []byte{}

    for i:=0; i<len(s); i++ {
        if (i+1 != len(s)) && (s[i+1]!=' ') {
            cnt++
            continue
        }
        end = i

        for j := 0; j <= cnt; j++ {
            arr = append(arr, s[end-j])
        }
        cnt = 0

        if i+1!=len(s) {
            arr = append(arr, ' ')
            i++
        }
    }
    return string(arr)
}

876. 链表的中间结点

给你单链表的头结点 head ，请你找出并返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 1：

img

输入：head = [1,2,3,4,5]
输出：[3,4,5]
解释：链表只有一个中间结点，值为 3 。
示例 2：

img

输入：head = [1,2,3,4,5,6]
输出：[4,5,6]
解释：该链表有两个中间结点，值分别为 3 和 4 ，返回第二个结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func middleNode(head *ListNode) *ListNode {
    slow, fast := head, head
    for fast!=nil && fast.Next!=nil {
        slow = slow.Next
        fast = fast.Next.Next
    }
    return slow
}

19. 删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

img

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]
示例 2：

输入：head = [1], n = 1
输出：[]
示例 3：

输入：head = [1,2], n = 1
输出：[1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func removeNthFromEnd(head *ListNode, n int) *ListNode {
    dummy := &ListNode{0, head}
    slow, fast := dummy, dummy
    for i:=0; i<n; i++ {
        fast = fast.Next
    }
    for fast.Next!=nil && fast!=nil {
        fast = fast.Next
        slow = slow.Next
    }
    slow.Next = slow.Next.Next
    return dummy.Next
}

滑动窗口

3. 无重复字符的最长子串

给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。

换句话说，s1 的排列之一是 s2 的 子串 。

示例 1：

输入：s1 = “ab” s2 = “eidbaooo”
输出：true
解释：s2 包含 s1 的排列之一 (“ba”).
示例 2：

输入：s1= “ab” s2 = “eidboaoo”
输出：false

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func checkInclusion(s1 string, s2 string) bool {
    n,m := len(s1),len(s2)
    if n > m {
        return false
    }
    cnt1, cnt2 := [26]int{}, [26]int{}
    for i := 0; i < n; i++ {
        cnt1[s1[i] - 'a']++
        cnt2[s2[i] - 'a']++
    }
    if cnt1 == cnt2 {
        return true
    }
    for i := n; i < m; i++ {
        cnt2[s2[i] - 'a']++
        cnt2[s2[i-n] - 'a']--
        if cnt1 == cnt2 {
            return true
        }
    }
    return false
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * @param {string} s1
 * @param {string} s2
 * @return {boolean}
 */
var checkInclusion = function(s1, s2) {
    const n = s1.length, m = s2.length
    if(n > m) {
        return false
    }
    let cnt1 = new Array(26).fill(0)
    let cnt2 = new Array(26).fill(0)
    for(let i = 0; i < n; i++) {
        cnt1[s1[i].charCodeAt() - 'a'.charCodeAt()]++
        cnt2[s2[i].charCodeAt() - 'a'.charCodeAt()]++
    }
    if(cnt1.toString() === cnt2.toString()) {
        return true
    }
    for(let i = n; i < m; i++) {
        cnt2[s2[i].charCodeAt() - 'a'.charCodeAt()]++
        cnt2[s2[i-n].charCodeAt() - 'a'.charCodeAt()]--
        if(cnt1.toString() === cnt2.toString()) {
            return true
        }
    }
    return false
};

567. 字符串的排列

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
示例 2:

输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
示例 3:

输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，”pwke” 是一个子序列，不是子串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func lengthOfLongestSubstring(s string) int {
    set := map[byte]int{}
    len := len(s)
    right, ans := -1, 0
    for i:=0;i<len;i++ {
        if i!=0 {
            delete(set, s[i-1])
        }
        for right+1<len && set[s[right+1]]==0 {
            set[s[right+1]]++
            right++
        }
        ans = max(ans, right+1-i)
    }
    return ans
}

func max(x, y int) int {
    if(x < y) {
        return y
    }
    return x
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * @param {string} s
 * @return {number}
 */
var lengthOfLongestSubstring = function(s) {
    const set = new Set()
    let right = -1, len = s.length, ans = 0
    for(let i = 0; i < len; i++) {
        if(i != 0) {
            set.delete(s.charAt(i-1))
        }
        while(right+1 < len && !set.has(s.charAt(right+1))) {
            set.add(s.charAt(right+1))
            right++
        }
        ans = Math.max(ans, right+1-i)
    }
    return ans
};

BFS/DFS

🧩733. 图像渲染

有一幅以 m x n 的二维整数数组表示的图画 image ，其中 image[i][j] 表示该图画的像素值大小。

你也被给予三个整数 sr , sc 和 newColor 。你应该从像素 image[sr[sc 开始对图像进行 上色填充 。

为了完成 上色工作 ，从初始像素开始，记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为 newColor 。

最后返回 经过上色渲染后的图像 。

img

示例 1:

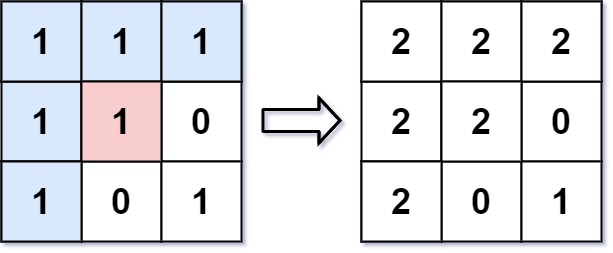
输入: image = [[1,1,1],[1,1,0],[1,0,1]]，sr = 1, sc = 1, newColor = 2
输出: [[2,2,2],[2,2,0],[2,0,1]]
解析: 在图像的正中间，(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。
注意，右下角的像素没有更改为2，因为它不是在上下左右四个方向上与初始点相连的像素点。
示例 2:

输入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2
输出: [[2,2,2],[2,2,2]]

解题思路

这是一个BFS/DFS典中典题！

已知：题目已经告诉我们 图像数组image(行列m*n)，起始点(sr, sc)，需求色color。

要求：将从该点起步，将自身以及其上/下/左/右方向上相邻色块中，不同于需求颜色的原始色更改，最后返回image数组。

思路(BFS)：

  1. 判断起始点颜色是否为需求色color。如果是，直接返回数组；反之，存储原始色rawColor，并将数组中对应值改为color值。
  2. 我们初始化一个队列queue = [{x: sr, y: rc}]，用于存放 被搜寻到的 且 颜色为rawColor 的色块。
  3. 接下来我们详细阐述此题广搜步骤：
    1. 将队列中首元素提出，颜色改为color值
    2. 分别搜索该元素上/下/左/右(对应x/y增减，四种)块中是rawColor且在图片范围内的元素，随后将其加入队列中，并改颜色
    3. 由于我们在这一次的搜索中，遍历了某一层元素的下一层元素，那么在下一次搜索中，我们需要将该层元素提取出来进行搜索
    4. 直至全部搜寻到(介时队列为空，长度为0)

以下是我算是 第一次用JS写BFS 代码+注释↓

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// BFS
var floodFill = function(image, sr, sc, color) {
    // 起始点颜色
    let rawColor = image[sr][sc]
    // 如果颜色一样直接返回
    if (rawColor === color) {
        return image
    }
    // 如果不一样，开始广搜
    let queue = [{x:sr, y:sc}],// 符合条件的像素块组成的队列（范围内，相邻，是起始颜色）
        dx = [0, 0, 1, -1],// 位移坐标
        dy = [1, -1, 0, 0],
        rowLen = image.length,// 图画长宽-图画边框范围
        colLen = image[0].length
    // 遍历队列
    while (queue.length != 0) {
        // 队列中首元素pop
        let {x, y} = queue.shift()
        // 首元素改颜色
        image[x][y] = color
        // 该元素相邻搜一下
        for (let i = 0; i < 4; i++) {
            // 相邻元素坐标
            let newX = x+dx[i], newY = y+dy[i]
            // 在画框范围内，且为起始颜色
            if(newX>=0 && newX<rowLen && newY>=0 && newY<colLen && image[newX][newY] == rawColor) {
                // 添加到队列中
                queue.push({x: newX, y: newY})
                // 且改变为要求颜色
                image[newX][newY] = color
            }
        }
    }
    return image
};

代码

这位佬写的代码超级简洁且优雅↓

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**
 * @param {number[][]} image
 * @param {number} sr
 * @param {number} sc
 * @param {number} color
 * @return {number[][]}
 */

// DFS
const floodFill = (image, sr, sc, newColor) => {
    const m = image.length;
    const n = image[0].length;
    const oldColor = image[sr][sc];
    if (oldColor == newColor) return image;

    const fill = (i, j) => {
        if (i < 0 || i >= m || j < 0 || j >= n || image[i][j] != oldColor) {
            return;
        }
        image[i][j] = newColor;
        fill(i - 1, j);
        fill(i + 1, j);
        fill(i, j - 1);
        fill(i, j + 1);
    };

    fill(sr, sc);
    return image;
};

// BFS
const floodFill = (image, sr, sc, newColor) => {
    const m = image.length;
    const n = image[0].length;
    const oldColor = image[sr][sc];

    if (oldColor == newColor) return image;

    const queue = [[sr, sc]];

    while (queue.length) {
        const [i, j] = queue.shift();
        image[i][j] = newColor;

        if (i - 1 >= 0 && image[i - 1][j] == oldColor) queue.push([i - 1, j]);
        if (i + 1 < m && image[i + 1][j] == oldColor) queue.push([i + 1, j]);
        if (j - 1 >= 0 && image[i][j - 1] == oldColor) queue.push([i, j - 1]);
        if (j + 1 < n && image[i][j + 1] == oldColor) queue.push([i, j + 1]);
    }

    return image;
};

🏝695. 岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

img

示例 1：

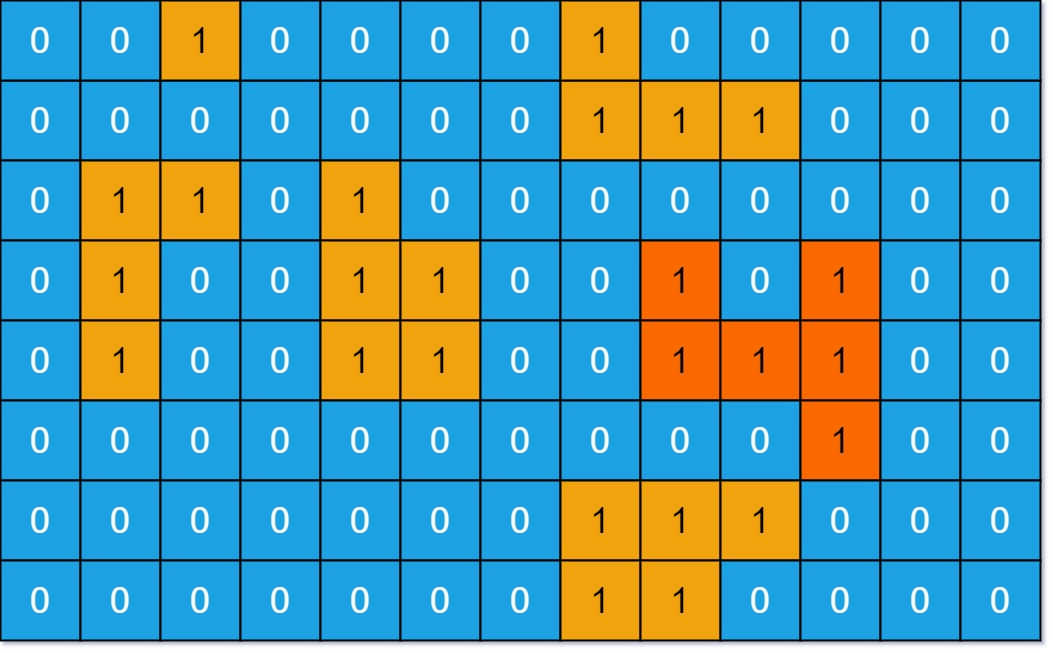
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

解题思路

已知：grid(m*n) 岛屿是1，水是0

要求：最大的岛屿面积ans（四个正方向相邻的1块才属于同一个岛屿）

思路:

  1. 此题较上题多了一层逻辑，那就是需要自行寻找起始点，我们不妨对grid这个二维数组套用行列遍历
  2. 随后进行广搜/深搜
  3. 那么这个题，让我们顺一下深搜步骤：
    1. 我们不妨声明一个 名为dfs的 返回ans值的 用来搞递归的 函数
    2. 当我们对一个元素进行上下左右搜索时，分别对搜索到的(符合条件的)元素进行上下左右搜索，←的同时对搜索到的元素进行上下左右搜索……
    3. 补充一个环节，那就是当搜索的元素不符合条件的时候，return 回溯到上一层（在本题中，返回ans值为0)

请直接移移步到大佬写的代码↓

代码

优雅太优雅了↓

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
/**
 * @param {number[][]} grid
 * @return {number}
 */

// 大佬的DFS
var maxAreaOfIsland = function(grid) {
    let ans = 0
    const m = grid.length, n = grid[0].length
    function dfs (x, y) {
        if(x < 0 || x >= m || y < 0 || y >= n || grid[x][y] === 0) return 0
        grid[x][y] = 0
        let ans = 1
        const dx = [0, 0, 1, -1], dy = [1, -1, 0, 0]
        for (let i = 0; i < 4; i++) {
            ans += dfs(x+dx[i], y+dy[i])
        }
        return ans
    }
    for(let i = 0; i < m; i++) {
        for(let j = 0; j < n; j++) {
            if(grid[i][j] === 0) continue
            ans = Math.max(ans, dfs(i, j))
        }
    }
    return ans
};

// 大佬的BFS
var maxAreaOfIsland = function(grid) {
    let ans = 0, row = grid.length, col = grid[0].length;
    let dx = [1, -1, 0, 0], dy = [0, 0, 1, -1];//方向数组
    for (let i = 0; i < row; i++) {
        for (let j = 0; j < col; j++) {
            if (grid[i][j] === 0) continue;//循环网格，遇到0就跳过
            let queue = [[i, j]], curr = 0;//在队列中加入当前网格的值
            while (queue.length > 0) {
                let [x, y] = queue.shift();//不断出队
              	//越界判断
                if (x < 0 || x >= row || y < 0 || y >= col || grid[x][y] === 0) continue;
                ++curr;//更新岛屿的数量
                grid[x][y] = 0;//遍历过的网格置为0
                for (let k = 0; k < dx.length; k++) {//上下左右遍历，把下一层的节点加入队列
                    queue.push([x + dx[k], y + dy[k]]);
                }
            }
            ans = Math.max(ans, curr);//更新最大岛屿面积
        }
    }
    return ans;
};

// 我的BFS——哥们儿就喜欢BFS（等待打脸）
var maxAreaOfIsland = function(grid) {
    let ans = 0, m = grid.length, n = grid[0].length
    const dx = [0, 0, 1, -1], dy = [1, -1, 0, 0]
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] === 0) {
                continue
            }
            let queue = [{x: i, y: j}], s = 1
            while (queue.length != 0) {
                let {x, y} = queue.shift()
                grid[x][y] = 0
                for (let k = 0; k < 4; k++) {
                    let newX = x + dx[k], newY = y + dy[k]
                    if (newX >= 0 && newY >= 0 && newX < m && newY < n && grid[newX][newY] == 1) {
                        queue.push({x: newX, y: newY})
                        grid[newX][newY] = 0
                        s++
                    }
                }
            }
            ans = Math.max(ans, s)
        }
    }
    return ans
};

🌲617. 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]
示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

解题思路

  1. 我们直接在root1上做修改，我们简称两者为一和二：

    1. 当仅一为空的时候，递归函数返回二
    2. 当仅二为空的时候，递归函数返回一
    3. 两者皆空依然返回一
    4. 两者都不空，那.val相加

  2. 调用函数本身，实现节点左右孩子合并

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {TreeNode}
 */
var mergeTrees = function(root1, root2) {
    if(!root1) {
        return root2
    }
    if(!root2) {
        return root1
    }
    root1.val += root2.val

    root1,left = mergeTrees(root1.left, root2.left)
    root1.right = mergeTrees(root1.right, root2.right)

    return root1
};
// 当然也可以新开一个树，不在原树上做更改。

👉116. 填充每个节点的下一个右侧节点指针

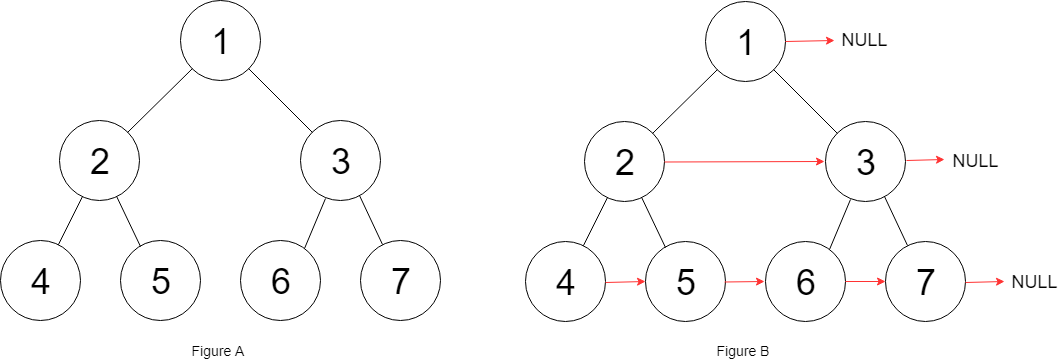
给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

img

输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，’#’ 标志着每一层的结束。
示例 2:（注意看这个看着像示例2的示例2）

输入：root = []
输出：[]

解题思路(层次遍历)

发现广搜深搜可以变简洁的小思路是先排除无效的，比如示例二这种

  1. 所以先排除root=null的情况
  2. 将根节点放入新开队列中，开始按层遍历
  3. 遍历过程中需要完成两项任务：
    1. 同层next赋值
    2. 将下一层增加到队列中

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * // Definition for a Node.
 * function Node(val, left, right, next) {
 *    this.val = val === undefined ? null : val;
 *    this.left = left === undefined ? null : left;
 *    this.right = right === undefined ? null : right;
 *    this.next = next === undefined ? null : next;
 * };
 */
/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function(root) {
    if (root === null) return root
    const queue = [root]
    while (queue.length > 0) {
        let size = queue.length
        for (let i = 0; i < size; i++) {
            let node = queue.shift()
            if (i < size - 1) {
                node.next = queue[0]
            }
            if (node.left !== null) {
                queue.push(node.left)
            }
            if (node.right !== null) {
                queue.push(node.right)
            }
        } 
    }
    return root
};

// 还有一种直接用.next
// node.right.next = node.left    node.right.next = node.next.left

🍊994. 腐烂的橘子

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4
示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。
示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

解题思路(BFS)

  1. 与烂橘子相邻的好橘子会在一分钟后腐烂
  2. 假设最开始所有的烂橘子是第0层，那么隔一分钟烂一层（其下层就是其上下左右方向的好橘子）
  3. 如果存在不挨着任何一个烂橘子的好橘子，返回-1；如果到最后都烂了，返回层数；如果一开始没有好橘子，返回0

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * @param {number[][]} grid
 * @return {number}
 */
var orangesRotting = function(grid) {
    // 好果子耶！
    let fresh = 0
    // 框定边界
    const row = grid.length, col = grid[0].length
    // 工具队列（专门盛放烂橘子）
    let que = []
    // 遍历筐内所有橘子，好的fresh+1，坏的添加到队列
    for (let i = 0; i < row; i++) {
        for (let j = 0; j < col; j++) {
            if(grid[i][j] === 1) {
                fresh++
            } else if (grid[i][j] === 2) {
                que.push([i, j])
            }
        }
    }
    // 位移数组
    const dx = [0, 0, 1, -1]
    const dy = [1, -1, 0, 0]
    // 找不到坏果子就不算0层（-1层）
    let cnt = -1
    // 按层遍历
    while (que.length) {
        // 层数+1
        cnt++
        // 每层烂橘子个数
        let size = que.length
        // 遍历cnt层
        for (let i = 0; i < size; i++) {
            // 去除一个当做父节点
            let [x, y] = que.shift()
            // 寻找自己的上下左右孩子（感染对象）
            for (let j = 0; j < 4; j++) {
                let newX = x + dx[j], newY = y + dy[j]
                if (newX < 0 || newY < 0 || newX >= row || newY >= col || grid[newX][newY] !== 1) continue
                // 找到一个感染对象！把它感染，并放进队列，好橘子个数fresh-1
                grid[newX][newY] = 2
                que.push([newX, newY])
                fresh--
            }
        }
    }
    // 如果还有好橘子-1；如果一开始就没好橘子0；好橘子都没了cnt
    return fresh > 0 ? -1 : (cnt <= 0 ? 0 : cnt)
};

？🎛542. 01 矩阵

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

img

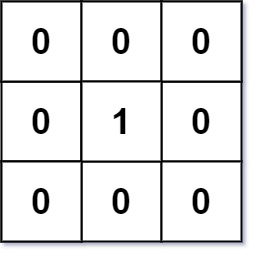
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]
示例 2：

img

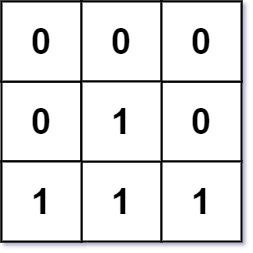
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

解题思路

此题用的动态规划

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * @param {number[][]} mat
 * @return {number[][]}
 */
var updateMatrix = function(mat) {
    if (!mat.length || !mat[0].length) return null

    const row = mat.length
    const col = mat[0].length

    let ans = new Array(row)
    for (let i = 0; i < row; i++) {
        ans[i] = new Array(col).fill(row + col)
    }

    for (let i = 0; i < row; i++) {
        for (let j = 0; j < col; j++) {
            if (mat[i][j] === 0) {
                ans[i][j] = 0
            }
        }
    }

    for (let i = 0; i < row; i++) {
        for (let j = 0; j < col; j++) {
            if (i - 1 >= 0) {
                ans[i][j] = Math.min(ans[i][j], ans[i - 1][j] + 1)
            }
            if (j - 1 >= 0) {
                ans[i][j] = Math.min(ans[i][j], ans[i][j - 1] + 1)
            }
        }
    }

    for (let i = row - 1; i >= 0; i--) {
        for (let j = col - 1; j >= 0; j--) {
            if (i + 1 < row) {
                ans[i][j] = Math.min(ans[i][j], ans[i + 1][j] + 1)
            }
            if (j + 1 < col) {
                ans[i][j] = Math.min(ans[i][j], ans[i][j + 1] + 1)
            }
        }
    } 
    return ans
};

递归/迭代

有的时候真的不理解递归，所以不喜欢用

但是多做几个就觉得很有成就感，又喜欢用了

👈️206. 反转链表

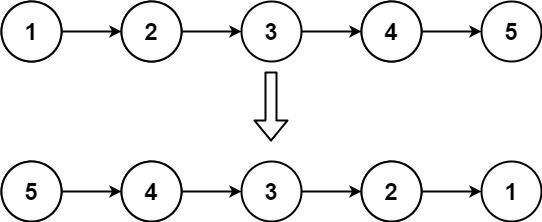
给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

img

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

解题思路(递归)

image-20230321184400708

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
// 递归
var reverseList = function(head) {
    if (head == null || head.next == null) {
        return head;
    }
    const newHead = reverseList(head.next);
    head.next.next = head;
    head.next = null;
    return newHead;
};

// 迭代
var reverseList = function(head) {
    let prev = null
    let curr = head
    while (curr) {
        const next = curr.next
        curr.next = prev

        prev = curr
        curr = next
    }
    return prev
};

🙏21. 合并两个有序链表

递归我的递归啊T_T

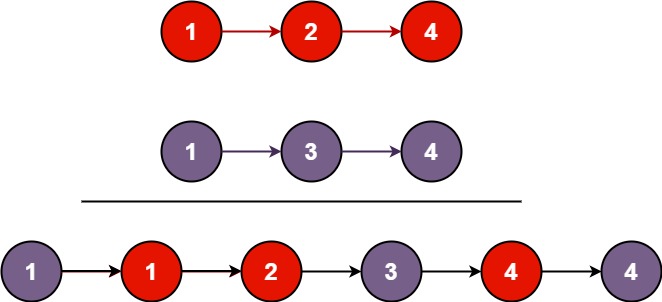
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

img 
1
2
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

1
2
输入：l1 = [], l2 = []
输出：[]

示例 3：

1
2
输入：l1 = [], l2 = [0]
输出：[0]

解题思路

  1. 当l1为空时返回剩下的l2
  2. 当l2为空时返回剩下的l1
  3. 当两者都不为空时，要继续递归，如果l1.val <= l2.val，那么递归参数将是(l1的下一个节点, l2)，返回l1
  4. 同理l2.val较小时递归l1与l2.next，返回l2

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} list1
 * @param {ListNode} list2
 * @return {ListNode}
 */
var mergeTwoLists = function(list1, list2) {
    if (!list2) return list1
    if (!list1) return list2
    if (list1.val <= list2.val) {
        list1.next = mergeTwoLists(list1.next, list2)
        return list1
    } else {
        list2.next = mergeTwoLists(list1, list2.next)
        return list2
    }
};

递归/回溯

用熟了就有点喜欢用了

👩‍👩‍👧‍👧46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

解题思路(回溯 DFS)

  1. DFS建树，排除重复重复解，搜出所有解
  2. 回溯入口：空数组传入
  3. 回溯过程：遍历数字（枚举各项），使用条件判断跳过剪枝项，将符合条件的项添加到数组中，进行下一次迭代选择
  4. 回溯出口：数组长度与定长长度一致

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function(nums) {
    const res = []
    const used = {}

    function dfs(path) {
        if (path.length == nums.length) {
            res.push(path.slice())
            return
        }
        for (const num of nums) {
            if (used[num]) continue

            path.push(num)
            used[num] = true

            dfs(path)

            path.pop()
            used[num] = false
        }
    }
    dfs([])
    return res
};

👪️77. 组合

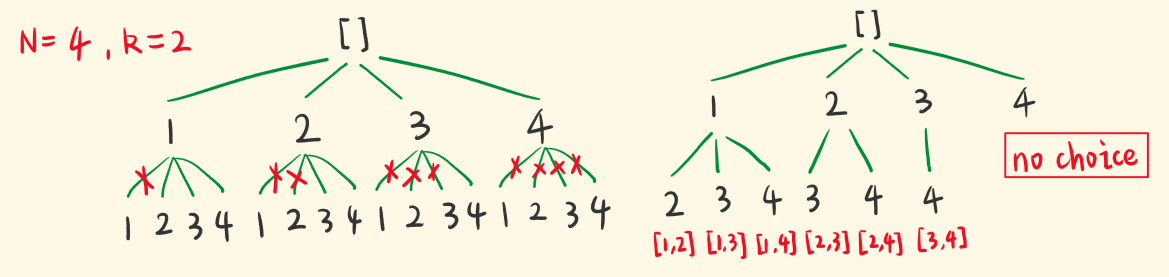
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2：

输入：n = 1, k = 1
输出：[[1]]

解题思路

大同小异，不过要注意此题要求的排列完全解不包含重复元素的不同排列(1,2 2,1 nono!)

所以我们需要通过控制枚举起点start，来正确裁剪分支

  1. 回溯起点：枚举起点1，空数组
  2. 回溯终点：队列长度与要求长度相等
  3. 回溯过程：枚举起点start在每一次迭代时+1

image.png

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function(n, k) {
    let ans = []
    let used = new Map()
    function dfs(start, que) {
        if (que.length == k) {
            ans.push(que.slice())
            return
        }
        
        for (let key = start; key <= n; key++) {
            if (used.has(key)) continue
            
            que.push(key)
            used.set(key)
            
            dfs(key+1, que)
            
            used.delete(key)
            que.pop()
        }
    }
    dfs(1, [])
    return ans
};

🔠784. 字母大小写全排列

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。

返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。

示例 1：

输入：s = “a1b2”
输出：[“a1b2”, “a1B2”, “A1b2”, “A1B2”]
示例 2:

输入: s = “3z4”
输出: [“3z4”,”3Z4”]

解题思路

可恶！！！数字！！！！树树树！！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * @param {string} s
 * @return {string[]}
 */
var letterCasePermutation = function(s) {
    let ans = []
    const len = s.length

    const dfs = (start, que) => {
        if (que.length == len) {
            ans.push(que.join(''))
            return
        }
        for (let i = start; i < len; i++) {
            if (s.charAt(i) >= '0' && s.charAt(i) <= '9') {
                // 遇到数字pushpushdfs
                que.push(s.charAt(i))
                dfs(i+1, que)
                que.pop()
            } else {
                // 遇到字母pushpushdfsdfs
                que.push(s.charAt(i).toLowerCase())
                dfs(i+1, que)
                que.pop()

                que.push(s.charAt(i).toUpperCase())
                dfs(i+1, que)
                que.pop()
            }
        }
    }

    dfs(0, [])
    return ans
};

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
// 我有点不能接收其他思路的感觉，很可怕
var letterCasePermutation = function (s) {
  s = s.toLowerCase()
  let arr = [s[0]];
  if (s[0].charCodeAt() > 96) arr.push(s[0].toUpperCase())
  for (let i = 1; i < s.length; i++) {
    arr = arr.map(word => word += s[i])
    if (s[i].charCodeAt() > 96) arr = arr.concat(arr.map(word => word.slice(0, -1) + s[i].toUpperCase()))
  }
  return arr
};

作者：alexYang
链接：https://leetcode.cn/problems/letter-case-permutation/solution/by-alexyang-wzkk/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。


// 官方核武器版本
var letterCasePermutation = function(s) {
    const ans = [];
    const dfs = (arr, pos, res) => {
        while (pos < arr.length && isDigit(arr[pos])) {
            pos++;
        }
        if (pos === arr.length) {
            res.push(arr.join(""));
            return;
        }
        arr[pos] = String.fromCharCode(arr[pos].charCodeAt() ^ 32);
        dfs(arr, pos + 1, res);
        arr[pos] = String.fromCharCode(arr[pos].charCodeAt() ^ 32);
        dfs(arr, pos + 1, res);
        }
    dfs([...s], 0, ans);
    return ans;
};

const isDigit = (ch) => {
    return parseFloat(ch).toString() === "NaN" ? false : true;
}


作者：LeetCode-Solution
链接：https://leetcode.cn/problems/letter-case-permutation/solution/zi-mu-da-xiao-xie-quan-pai-lie-by-leetco-cwpx/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

动态规划

自下而上的超牛思想，使问题简单，促人生成功(doge)

🛤️70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

  1. 1 阶 + 1 阶
  2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

  1. 1 阶 + 1 阶 + 1 阶
  2. 1 阶 + 2 阶
  3. 2 阶 + 1 阶

解题思路

有两种方式上楼：一次迈一阶/一次迈两阶

最后一次上楼还剩 一阶/两阶

最近一次上楼方式总数 应该是 在此之前两种方式上楼方式的总和
$$
f(x) = f(x - 1) + f(x - 2)
$$
用脚趾推算得f(0) = f(1) = 1

那么接下来就可以遍历相加了

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function(n) {
    let ans = 0, step1 = 1, step2 = 0
    for (let i = 0;  i <= n; i++) {
        step2 = step1
        step1 = ans
        ans = step1 + step2
    }
    return ans
};

// 使用数组更适合我这种笨笨脑
var climbStairs = function(n) {
    let ans = new Array(n+1).fill(0)
    ans[0] = 1
    ans[1] = 1
    for (let i = 2;  i <= n; i++) {
        ans[i] = ans[i - 1] + ans[i - 1]
    }
    return ans[n]
};

🗼120. 三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

解题思路

浅画草图

IMG_20230323_091839

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * @param {number[][]} triangle
 * @return {number}
 */
var minimumTotal = function(triangle) {
    const row = triangle.length
    
    if (row === 1) {
        return triangle[0][0]
    }

    for (let i = row - 2; i >= 0; i--) {
        for (let j = 0; j < triangle[i].length; j++) {
            triangle[i][j] += Math.min(triangle[i+1][j], triangle[i+1][j+1])
        }
    }
    return triangle[0][0]
};

🕲198. 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。

解题思路

2 1 1 2

就是说问题可以拆分成两种情况↓：

  • 偷这个家-前头那家不能偷 (小偷溜达到这家，手里有前几家的米，并且攥了一把这家的米)
  • 偷前头那家-这家不能偷 (小偷溜达到这家的时候，手里有偷前前头那几家的米)

所以说状态量应该是：小偷溜达到第几家的时候手里有多少米

最终解是俩两种情况里挑最大的↓

2 1 1 2

偷2不偷0 偷1不偷2 偷3不偷2 偷4不偷3

那么↓

$home[x] = max(home[x-1], home[x-2] + money[x])$

小偷我到这家手里的钱钱 = 上一家偷来的钱钱 / 这家偷的钱钱和非上一家偷来的钱钱之和 (聪明的小偷会选择较大的获益)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * @param {number[]} nums
 * @return {number}
 */
var rob = function(nums) {
    let len = nums.length
    let dp = [nums[0], Math.max(nums[0], nums[1])]
    for (let i = 2; i < len; i++) {
        dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i])
    }
    return dp[len - 1]
};

// 状态压缩
var rob = function(nums) {
    if (nums.length === 1) {
        return nums[0]
    }

    let dp_0 = nums[0]
    let dp_1 = Math.max(nums[0], nums[1])
    let dp_max = dp_1

    for (let i = 2; i < nums.length; i++) {
        dp_max = Math.max(dp_1, dp_0 + nums[i])
        dp_0 = dp_1
        dp_1 = dp_max
    }

    return dp_max
};

位运算

1️⃣191. 位1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（汉明重量）。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在 示例 3 中，输入表示有符号整数 -3。

示例 1：

输入：n = 00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1’。
示例 2：

输入：n = 00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 ‘1’。
示例 3：

输入：n = 11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 ‘1’。

解题思路

观察：n & (n - 1) = 把n的二进制位中最低位的1变为0后的结果

也就是说我们只需要 不断把二进制数中的1=>0，直到数字变为0 就可以求得其“汉明重量/汉明权重”

​ 汉明权重是一串符号中不同于（定义在其所使用的字符集上的）零符号（zero-symbol）的个数。对于一个二进制数，它的汉明权重就等于它 1 的个数（即 popcount)。

代码

1
2
3
4
5
6
7
8
9
10
11
12
/**
 * @param {number} n - a positive integer
 * @return {number}
 */
var hammingWeight = function(n) {
    let popCount = 0
    while (n) {
        n &= n - 1
        popCount++
    }
    return popCount
};

2️⃣231. 2 的幂

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

示例 1：

输入：n = 1
输出：true
解释：20 = 1
示例 2：

输入：n = 16
输出：true
解释：24 = 16
示例 3：

输入：n = 3
输出：false
示例 4：

输入：n = 4
输出：true
示例 5：

输入：n = 5
输出：false

解题思路

我对位运算没太有概念啊，反正遇到一个题就记一下了

代码

1
2
3
4
5
6
7
8
9
10
11
/**
 * @param {number} n
 * @return {boolean}
 */
var isPowerOfTwo = function(n) {
    return n > 0 && (n & (n - 1)) === 0
};

var isPowerOfTwo = function(n) {
    return n > 0 && (n & (-n)) === n
}

🔢136. 只出现一次的数字

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

示例 1 ：

输入：nums = [2,2,1]
输出：1
示例 2 ：

输入：nums = [4,1,2,1,2]
输出：4
示例 3 ：

输入：nums = [1]
输出：1

解题思路

异或运算⊕有以下三个性质:

  1. $a ⊕ 0 = a$
  2. $a⊕a = 0$
  3. $ a ⊕ b ⊕ a = b ⊕ a ⊕ a = b ⊕ (a ⊕ a) = b ⊕ 0 = b $

所以只需要遍历数组，把所有的数进行异或，就可以找出只出现一次的数值。

代码

1
2
3
4
5
6
7
8
9
10
11
/**
 * @param {number[]} nums
 * @return {number}
 */
var singleNumber = function(nums) {
    let ans = 0
    for (let n of nums) {
        ans ^= n
    }
    return ans
};

#️⃣190. 颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在 示例 2 中，输入表示有符号整数 -3，输出表示有符号整数 -1073741825。

示例 1：

输入：n = 00000010100101000001111010011100
输出：964176192 (00111001011110000010100101000000)
解释：输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。
示例 2：

输入：n = 11111111111111111111111111111101
输出：3221225471 (10111111111111111111111111111111)
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。

解题思路

根据位运算特性，遍历各位，逐位颠倒。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * @param {number} n - a positive integer
 * @return {number} - a positive integer
 */
var reverseBits = function(n) {
    // 这个是运用JS内置一些API做的，但是效率不及后者
    // return +('0b'+n.toString(2).padStart(32,0).split('').reverse().join(''))
    
    let rev = 0 // 初始化一个放各位数的容器
    for (let i = 0; i < 32 && n > 0; i++) {  // 对n进行取数位移操作
        rev |= (n & 1) << (31 - 1)  // 取出n中最后一位数，并将该数放进dev指定位置
        n >>>= 1  // n无符号向右移动一位捏嘿
    }
    return rev >>> 0  // 一开始没加>>>0，报错了，错误案例是一个负数，我？？？ 
};
// 还有一种方法是‘位运算分治’我不太理解，偶数对调隔2对调隔4对调什么的