979. 在二叉树中分配硬币

邪门二叉树+DFS，根本设计不出来，图解那么巧妙，我直接大口啃菜。菜狗

题目要求大致：

给你一个二叉树，每个节点有随机数量个硬币，要求通过父子传递一次一硬币的方式使二叉树内节点上的硬币数量全部分成1。

先放代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var distributeCoins = function(root) {
    let sum = 0
    function dfs(node) {
        if (node === null) {
            return 0
        }

        let leftMove = 0,
            rightMove = 0
        if (node.left !== null) {
            leftMove = dfs(node.left)
        }
        if (node.right !== null) {
            rightMove = dfs(node.right)
        }

        sum += Math.abs(leftMove) + Math.abs(rightMove)

        return nodeMove = leftMove + rightMove + node.val - 1
    }

    dfs(root)
    return sum
};

后顺思路：

  • 自下而上确定变量
    • 叶子结点：自身需要向父节点移动(拿/出)多少次硬币
    • 每层根节点：左孩子需要从根节点移动多少次硬币，右孩子需要从根节点移动多少次硬币，出来好孩子的事情后自己还需要向父节点移动多少次硬币
    • sum值：用来记录每层移动硬币次数和
  • 确定变量之间的关系
    • 子节点会向父节点拉扯一下，举个例子：(0)-2-(0)，那么左上入1右上入1，父下出2，剩0，此时父需要上入1。
    • 以此类推往上排
  • 确定函数实现方式
    • 函数递归：深搜啦~
    • 全局sum记录：放在全局，调用的函数会操作它，程序最后返回
    • 处理特殊情况：null/边界值(名词乱用了属于是)

想画点图：

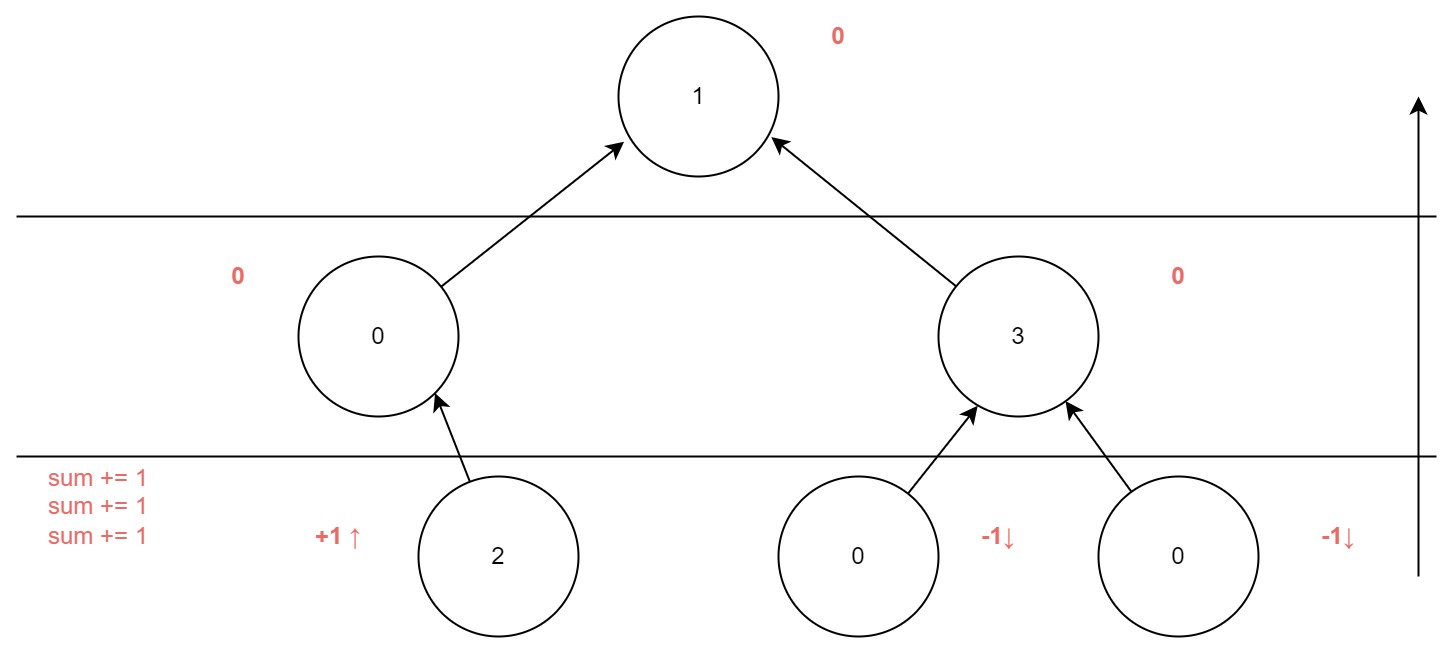
二叉树例子

834. 树中距离之和

笨死我了，两次深搜，还是二叉树，又是啃菜的一天……菜狗可恶不信多看几遍题解多敲一下脑子一点褶皱都不长！

大佬题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[]}
 */
var sumOfDistancesInTree = function(n, edges) {
    // 邻接关系表
    const graph = new Array(n)
    for (let i = 0; i < graph.length; i++) {
        graph[i] = [];
    }
    for (let edge of edges) {
        const [from, to] = edge
        graph[from].push(to)
        graph[to].push(from)
    }

    // 节点所在子树的节点个数
    let nodeNum = new Array(n).fill(1)
    // 节点到其所在子树节点的距离和 节点到其他所有节点的距离和
    let distNum = new Array(n).fill(0)

    // 子节点距离-后序-递归
    const postOrder = (root, parent) => {
        // 该节点的所有邻居节点
        const neighbors = graph[root]
        // 该节点每个子节点递归
        for (const neighbor of neighbors) {
            if (neighbor === parent) {
                continue
            }
            postOrder(neighbor, root)

            nodeNum[root] += nodeNum[neighbor]
            distNum[root] += distNum[neighbor] + nodeNum[neighbor]
        }
    }
    // 节点先序-递归
    const preOrder = (root, parent) => {
        // 该节点的所有邻居节点
        const neighbors = graph[root]
        // 该节点每个子节点递归
        for (const neighbor of neighbors) {
            if (neighbor === parent) {
                continue
            }
            distNum[neighbor] = distNum[root] - nodeNum[neighbor] + (n - nodeNum[neighbor])
            preOrder(neighbor, root)
        }
    }

    postOrder(0, -1)
    preOrder(0, -1)
    return distNum
};